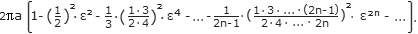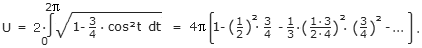

Der exakte Umfang der Ellipse mit der großen Halbachse a
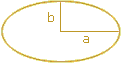
 gegeben. Solche Integrale kann man jedoch nicht elementar berechnen.
gegeben. Solche Integrale kann man jedoch nicht elementar berechnen.
 · (a+b)/2 -
· (a+b)/2 -  · √a
· b
bestimmen. Hieraus ergibt sich etwa für a = 5/4 und b = 1 der Näherungswert 7,0904... Dieser
stimmt mit dem exakten Umfang bis zur 4. Kommastelle überein.
Für besonders gestreckte oder gestauchte
Ellipsen ist diese Methode aber viel zu ungenau, wie unser folgendes Beispiel zeigt:
· √a
· b
bestimmen. Hieraus ergibt sich etwa für a = 5/4 und b = 1 der Näherungswert 7,0904... Dieser
stimmt mit dem exakten Umfang bis zur 4. Kommastelle überein.
Für besonders gestreckte oder gestauchte
Ellipsen ist diese Methode aber viel zu ungenau, wie unser folgendes Beispiel zeigt:
 ,
ist hingegen kleiner als 41.
,
ist hingegen kleiner als 41.
 .
Der Umfang U der Ellipse, also die volle Bogenlänge,
entspricht somit dem Integral
.
Der Umfang U der Ellipse, also die volle Bogenlänge,
entspricht somit dem Integral
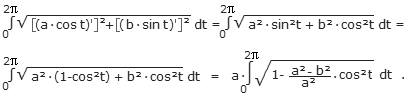
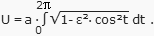
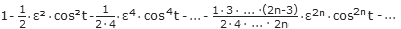
 ]
gleichmäßig(!) gegen f(t).
Hieraus folgt, dass die Reihe der Einzelintegrale
∑∫fi(t) dt gegen
∫f(t) dt
in den Grenzen
[0; 2
]
gleichmäßig(!) gegen f(t).
Hieraus folgt, dass die Reihe der Einzelintegrale
∑∫fi(t) dt gegen
∫f(t) dt
in den Grenzen
[0; 2 ]
konvergiert.
Wir müssen also „nur noch” die Integrale der einzelnen Reihenglieder berechnen.
]
konvergiert.
Wir müssen also „nur noch” die Integrale der einzelnen Reihenglieder berechnen.