Mit dem Begriff  „Kegel”  ist meist ein gerader Kreiskegel gemeint, der durch Radius R und Höhe H eindeutig bestimmt ist. Schneidet man ihn der Länge nach auf und rollt ihn ab, erhält man einen Kreissektor mit Radius M = √R²+H² und Winkel α = 2π·R/M. Umgekehrt liefert ein Kreissektor mit Radius M und Winkel α = 2π/n einen Kegel mit Radius R = M/n und Höhe H = √n²-1·M/n. So erhält man aus dem Halbkreis mit Radius R = 1 den Kegel mit Radius R = ½ und Höhe H = ½·√3.

Auf ähnliche Weise lässt sich ein Kegelstumpf konstruieren:

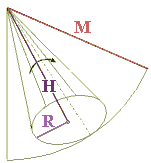
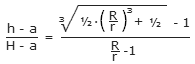Bemerkung

Wir befassen uns nun mit dem „Problem” des halbvollen Glases:
Hier ist die Füllhöhe h eines kegelförmigen Glases so zu bestimmen, dass gilt: ½·R²·π·H/3 = x²·π·h/3. Der Strahlensatz besagt: h/H = x/R, daher ist x = h·R/H. Somit können wir x² durch (h·R/H)² ersetzen und erhalten h/H = 2^-1/3. Ein kegelförmiges Glas ist also bei rund 80% Füllhöhe halbvoll.

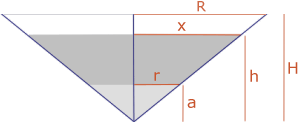
Wenn unser Glas jetzt ein Kegelstumpf ist - die skizzierte hellgraue Fläche ist dann massiv - entspricht „halbvoll” der Gleichung ½·(R²·H - r²·a)·π/3 = (x²·h - r²·a)·π/3. Daraus folgt: H·R² + a·r² = 2h·x². Der Strahlensatz liefert: x = h·r/a sowie R/r = H/a und somit gilt: 2h³ = H³+a³. Ebenso zeigt der Strahlensatz: a = H·r/R = r·(H-a)/(R-r), also gilt: H = (H-a)·R/(R-r). Mit Hilfe dieser Gleichungen und elementarer Umformungen erhalten wir nun den Quotienten aus gesuchter und maximaler Füllhöhe:

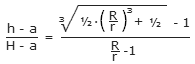
Allein aus dem Verhältnis der beiden Radien kann man somit ermitteln, wann ein Kegelstumpf zur Hälfte gefüllt ist, wie etwa beim rechts dargestellten Glas. Der obere Radius R ist hier ungefähr fünfmal größer als der untere Radius r. Folglich beträgt unser Quotient (h-a)/(H-a) zirka (63^1/3-1)/4, also rund 3/4. Der gegebene Pegelstand liegt aber offensichtlich unterhalb der erforderlichen 75% der maximalen Füllhöhe. Im Widerspruch zum spontanen optischen Eindruck ist unser Glas daher weniger als halbvoll. Dagegen konvergiert für R/r  →  1 (Zylinder) der Quotient (h-a)/(H-a) natürlich gegen ½.