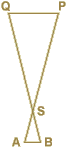Die Seitenverhältnisse zweier ähnlicher Dreiecke sind immer gleich - legt man beide Dreiecke aufeinander oder die Ecken passend aneinander, ergeben sich die sogenannten
Strahlensätze:
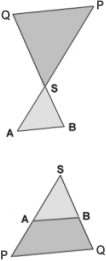
Wenn zwei Strecken (Strahlen) mit gemeinsamen Schnittpunkt S von einem Paar paralleler
Strecken gekreuzt werden, dann gilt:
1. Strahlensatz: SA : SP = SB : SQ.
2. Strahlensatz: SA : SP = AB : PQ.
Unter Einbeziehung der Relationen:
|AP| = |SP| ± |SA| und |BQ| = |SQ| ± |SB| erhält man
folgende Aussagen:
SP : AP = SQ : BQ,
SA : AP = SB : BQ.
Frage
Im freien Gelände kann man Entfernungen ohne technische Hilfe mit dem Daumensprung
messen. Ich strecke den Arm ganz nach vorne, halte den Daumen hoch und kneife
erst das eine und dann das andere Auge zu. Dabei springt der Daumen vor dem
anvisierten Objekt um die Strecke Z hin und her. Mein Abstand
zu dem Objekt beträgt dann 10×Z.
Beispiel: Ich stehe am Strand und sehe ein 100 Meter langes Schiff an mir
vorbeifahren. Wenn das Schiff zweimal zwischen den Daumensprung
passt, dann ist Z = 200 Meter, womit seine Entfernung 2000 Meter beträgt.
Ist das mathematisch korrekt?
Antwort
Die Abschätzung ist einwandfrei,
falls die Strecke Z zwischen den beiden anvisierten Punkten parallel zur Augenlinie ist:
In unserer Skizze stehen die Eckpunkte A und B für die beiden Augen.
Der Schnittpunkt S ist die Daumenspitze, mit der man den Punkt P bzw. Q
im Visier hat.
Wenn jetzt die Augenlinie AB und die Verbindungsstrecke PQ
(= Z)
parallel sind, dann stimmen die Seitenverhältnisse in den Dreiecken überein und daraus folgt:
SA : AB = SP : PQ.
Setzt man nun voraus, dass der Abstand |SA| vom Daumen zum Auge das Zehnfache des Augenabstands |AB|
beträgt, so gilt: |SP| = 10
·|PQ|.