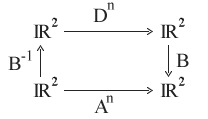
Wir wollen eine Basis (u, v) des IR² bestimmen, so dass die Matrix A bzw. der korrespondierende Endomorphismus h bezüglich der Vektoren u, v einer Diagonalmatrix

entspricht. Damit ist gefordert: h(u) = λ·u + 0·v und h(v) = 0·u + μ·v. Daraus folgt: A·u = λ·E·u, wobei E die 2×2-Einheitsmatrix ist. Daher wird u ≠ 0 von (A - λ·E) auf den Nullvektor abgebildet. Der Endomorphismus (A - λ·E) ist somit nicht injektiv, daraus folgt: det(A - λ·E) = 0. Ebenso gilt: det(A - μ·E) = 0. Die Zahlen λ, μ sind also die Nullstellen des Polynoms φ(x):= det(A - x·E) = x² - x - 1 (die Komponenten von A - x·E sollte man hier als Elemente des Körpers IR(x) auffassen). Das Polynom φ ist von der Wahl der Basis unabhängig - man nennt es deshalb das „charakteristische Polynom” von h. Seine Nullstellen λ = ½ + ½·√5 und μ = ½ - ½·√5 nennt man „Eigenwerte” und die Vektoren u, v mit A ·u = λ·u bzw. A·v = μ·v heißen „Eigenvektoren”. Per Additionsverfahren erhalten wir:

die (bis auf ein skalares Vielfaches eindeutig bestimmten) Vektoren u,v sind linear unabhängig und bilden daher eine Basis des IR². In Bezug auf diese Basis korrespondiert der Endomorphismus h also zur Diagonalmatrix

Die Potenzen von D kann man mühelos explizit angeben, womit wir unser Ziel, nämlich das Bild des Startvektors w := (a₁, a₀)^t unter der linearen Abbildung Aⁿ zu berechnen, fast erreicht haben. Allerdings beziehen sich die Koordinaten a₁, a₀ auf die kanonische Basis des IR², während sich die Diagonalmatrix D und ihre Potenzen auf die Basisvektoren u, v beziehen. Die entsprechenden Koordinaten a₀' und a₁' erhalten wir durch Lösung des Gleichungssystem u·a₁' + v·a₀' = w, also durch die Lösung der Gleichung B·w' = w, wobei u, v die Spalten der Matrix B sind und w':= (a₁', a₀' )^t ist. Somit gilt: w' = B^-1·w, daher liefert Dⁿ·B^-1·w die explizite Auflösung der Fibonaccifolge. Es fehlt noch die Rücktransformation in das ursprüngliche Koordinatensystem, was wir durch Multiplikation mit der Matrix B erreichen. Das folgende kommutative Diagramm skizziert die Situation, die von der Wahl des Vektors w unabhängig ist:

Damit ist auch die Gleichung: Aⁿ = B·Dⁿ·B^-1 anschaulich begründet.