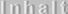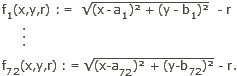Gleichungssysteme mit mehr Gleichungen als Unbekannten bezeichnet man als überbestimmt, und
im Allgemeinen sind solche Systeme nicht lösbar. Beispielsweise ergibt sich aus
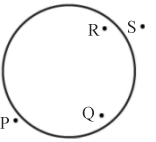 Sucht man etwa unter allen Kreisen der Ebene denjenigen,
der zu den vier Punkten P, Q, R, S die kleinste Summe von Abstandsquadraten hat - die
euklidische Norm des Fehlers ist dann minimal - wird vorab ein geeigneter Schätzwert für
den Mittelpunkt und den Radius benötigt. Damit kann man das Problem linearisieren, hier also auf die Lösung
linearer Gleichungssysteme reduzieren:
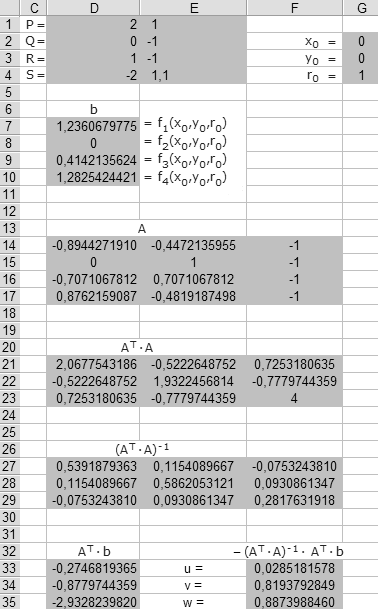
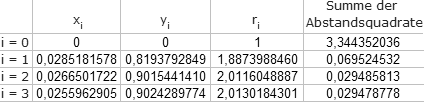
Sucht man etwa unter allen Kreisen der Ebene denjenigen,
der zu den vier Punkten P, Q, R, S die kleinste Summe von Abstandsquadraten hat - die
euklidische Norm des Fehlers ist dann minimal - wird vorab ein geeigneter Schätzwert für
den Mittelpunkt und den Radius benötigt. Damit kann man das Problem linearisieren, hier also auf die Lösung
linearer Gleichungssysteme reduzieren:
2x + 3y = 1
4x + 3y = 5
3x + 6y = 1